区间第K大
题目大致意思是Q个询问,每次询问一个K,输出表示第K年应该由那个城市举办奥运会。
举办奥运会的次序是由举办次数决定的,举办次数少的优先举办,同等次数编号小的优先。并且前N年的举办情况已经知道。
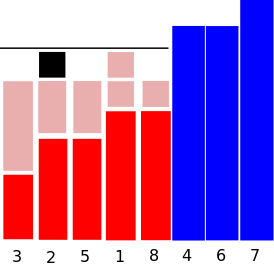
我们可以先对前n年的城市举办的次数从小到大排序。其实我们可以发现举办的过程就是不断的去填平每一行,使得它们的差距不断减小。
S[n]数组, 表示 i 前面每一列与第i列持平(填数是一行一行填的,目的是得到每一列相持平),所需要的年数。可以发现k在某一区间内都是填固定的区间 . 填至与第i列高度持平.然后转向区间 继续这样填。
有了S数组我们可以二分找到它正在填的区间,比如二分找到了位置pos,即它当前正在填区间 ,我从2开始计算S数组,所以区间右端点为 pos-1 (注意我所说的区间是指按照前N年出现次数排序后的区间)。找到了所填区间,我们就可以对区间长度 pos-1 取模,取模的得到的数X,正是它在填这个区间内的第X大数。然后转化为主席树求解(平衡时也可以,不过暂时不会)。
#include<stdio.h>
#include<string.h>
#include<queue>
#include<algorithm>
#include<iostream>
using namespace std;
const int N = 5e5 + 10;
typedef long long ll;
int n, m, q;
struct node{
int val, pos;
bool operator<(const node &o)const{
return val < o.val;
}
}a[N];
struct Tree{
int lc, rc, cnt;
}T[N<<5];
ll s[N];
int ct[N];
int tot,up;
int root[N];
void update(int &cur, int pre, int l, int r, int pos)
{
cur = ++tot;
T[cur] = T[pre];
T[cur].cnt++;
if (l == r) return;
int mid = (l + r) >> 1;
if (pos <= mid) update(T[cur].lc, T[pre].lc, l, mid, pos);
else update(T[cur].rc, T[pre].rc, mid + 1, r,pos);
}
int query(int x, int y, int l, int r, int k)
{
if (l == r) return l;
int s = T[T[y].lc].cnt - T[T[x].lc].cnt;
int mid = (l + r) >> 1;
if (k <= s)
return query(T[x].lc, T[y].lc, l, mid, k);
else
return query(T[x].rc, T[y].rc, mid + 1, r, k-s);
}
int main()
{
up = 5e5 + 5;
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i++)
{
int x;
scanf("%d", &x);
ct[x]++;
}
for (int i = 1; i <= m; i++)
{
a[i].val = ct[i];
a[i].pos = i;
}
sort(a + 1, a + m + 1);
for (int i = 2; i <= m; i++)
{
s[i] = s[i - 1] + (i - 1LL)*(a[i].val - a[i - 1].val); //一定要转化为LL,不然爆int
}
for (int i = 1; i <= m; i++)
{
update(root[i], root[i - 1], 1, up, a[i].pos);
}
while (q--)
{
ll k;
scanf("%lld", &k);
k -= n;
int pos = lower_bound(s + 1, s + m + 1, k) - s;//先找到区间
k = (k - s[pos - 1] - 1) % (pos - 1) + 1; //先减去前pos-1个区间所需的年数,然后再取模得到区间第K大
int ans = query(root[0], root[pos - 1], 1, up, k);//
printf("%d\n", ans);
}
return 0;
}

评论